Answer:
C
Explanation:
Consider the trinomial
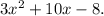
We can rewrite it as
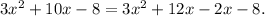
Now group first two terms and last two terms:
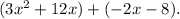
The common factor in first two terms is
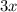 and the common factor in last two terms is
and the common factor in last two terms is
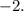 Use the distributive property for both groups of terms:
Use the distributive property for both groups of terms:
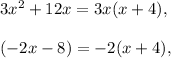
so
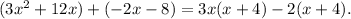
Now you can see that
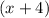 is a common factor, thus
is a common factor, thus

Since the trinomial can be represented as a product of binomials, this trinomial is not prime.