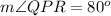1 Answer

Prophet · Answer 1 · 2020-04-26T08:23:05+0000

Answer:

m∠QPR = 80°

Explanation:

Look at the picture.

We know: the sum of the measures of the angles of the triangle is equal to 180 °.

Therefore

In ΔTQR we have the equation:

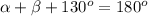$\alpha+\beta+130^o=180^o$ subtract 130° from both sides

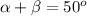
$\alpha+\beta=50^o$

In ΔPQR we have the equation:

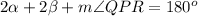
$2\alpha+2\beta+m\angle QPR=180^o$

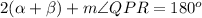
$2(\alpha+\beta)+m\angle QPR=180^o$

Substitute from the first equation

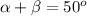
$\alpha+\beta=50^o$

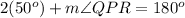
$2(50^o)+m\angle QPR=180^o$

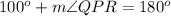$100^o+m\angle QPR=180^o$ subtract 100° from both sides

$m\angle QPR=80^o$