Answer:

Explanation:
Given :
The revenue, in dollars, of a company that makes toy cars can be modeled by the polynomial
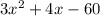
The cost, in dollars, of producing the toy cars can be modeled by
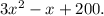
To Find: Profit function
Solution:
Revenue =
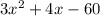
Cost = tex]3x^2 -x + 200[/tex]
Now we are supposed to find the profit
So, Profit = Revenue - Cost
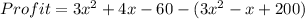
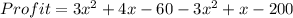
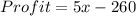
Hence The expression represents the profit is
