Answer:
Let's go through the following example to show how to solve a system of equations by graphing. I won't solve this system, I will just show how to.
If you can use an online graphing calculator...
If you have an online grapher (like Desmos) at your disposal, then you can put each equation in it as it is.
- Lines intersect -> Put your cursor over the point of intersection to get the solution.
- Lines never intersect -> The lines are parallel and there is no solution
- Lines perfectly fall on each other -> The lines are the same and have infinite solutions
If you have a physical graphing calculator (like TI-84)
1. Get both equations in the form
 by solving for y.
by solving for y.
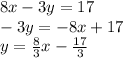

2. Put both equations in the graphing calculator
- Lines intersect -> Find the intersection point using your graphing calculator's mechanics (each one is a little different)
- Lines never intersect -> The lines are parallel and there is no solution
- Lines perfectly fall on each other -> The lines have the same equation and have infinite solutions
If you just have graphing paper...
1. Get both equations into the form
 by solving for y.
by solving for y.
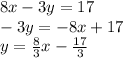

2. Plug in a few different points for x and calculate their y-values.
3. Plot those points on the graph paper
- Lines intersect -> Find the intersection point's coordinates to get the solution for x and y.
- Lines never intersect -> The lines are parallel and there is no solution
- Lines perfectly fall on each other -> The lines have the same equation and have infinite solutions.