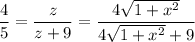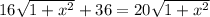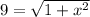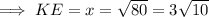Question

Given: Circles k1(A) and k2(O)ext. tangent

KE- tangent to k1(A) and k2(O)
AK=5, OE=4 Find: KE

There is a visual

Answer 1

AO is a line segment containing the radii of both circles, which are AK and OE, so AO = AK + OE = 9.

Extend AO to a point P on the line KE. Then we get two similar triangles APK and OPE. Let
`x` be the length of KE,
`y` the length of EP, and
`z` the length of OP.

By similarity, we have

`(OE)/(AK)=(EP)/(KP)=(OP)/(AP)\iff\frac45=\frac y{y+x}=\frac z{z+9}`

OPE is a right triangle, so

`OP^2=OE^2+EP^2\implies z=√(16+y^2)`

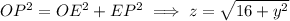
Now,

`\frac45=\frac y{y+x}\implies 4(y+x)=5y\implies 4x=y`

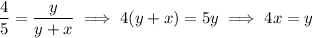
and we also have

`z=√(16+(4x)^2)=√(16+16x^2)=4√(1+x^2)`

Substituting this into the expression containing
`z` gives us an equation that we can solve for
`x`:

`\frac45=\frac z{z+9}=(4√(1+x^2))/(4√(1+x^2)+9)`

`16√(1+x^2)+36=20√(1+x^2)`

`9=√(1+x^2)`

`\implies KE=x=√(80)=3√(10)`