Question

2. The two figures are similar.

a) Write the similarity statement.
b) Is the image of the dilation a reduction or an enlargement of the original figure? Explain.
c) What is the scale factor? Explain.

Answer 1

Answer:(A) ab/a’b’=bc/b’c’=ac/a’c’ (B) Figure a’b’c’ is an enlargement because it increase it’s sides larger than 1. (C) So we have to divide to get the scale factor for both of these figures 18/6=3 then you found the scale factor 3.

Explanation:

Answer 2

Part a)
`(AB)/(A'B')=(BC)/(B'C') =(AC)/(A'C')`

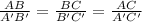
Part b) The dilation is an enlargement, because the corresponding sides of the image are larger than the corresponding sides of the original figure.(the scale factor is greater than 1)

Part c) The scale factor is
`3`

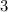
Explanation:

Part a) Write the similarity statement

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional

so

`(AB)/(A'B')=(BC)/(B'C') =(AC)/(A'C')`

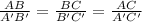
substitute the values

`(9)/(27)=(12)/(36) =(15)/(45')`

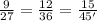
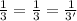`(1)/(3)=(1)/(3) =(1)/(3')` ----> is true

therefore

the figures are similar

Part b) The dilation is an enlargement, because the corresponding sides of the image are larger than the corresponding sides of the original figure. (the scale factor is greater than 1)

Part c) we know that

If two figures are similar, then the ratio of its corresponding sides is equal to the scale factor

Let

z------> the scale factor

x-----> corresponding side of the image

y------> corresponding side of the original figure

so

`z=(x)/(y)`

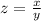
we have

`x=A'B'=27\ units`

`y=AB=9\ units`

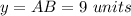
substitute

`z=(27)/(9)=3`

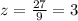
The scale factor is greater than 1

therefore

Is an enlargement