Answer:
EQUATION:
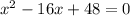
METHOD: Factorization.
The sellings prices are:
$4
$12
Explanation:
You need to find the selling price or prices that would generate $50 in daily profit, then you need to substityte
 into the quadratic function:
into the quadratic function:
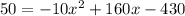
Make the equation equal to zero:
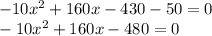
Simplify by dividing by -10, then you obtain the equation:
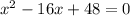
You can solve it with Factorization.
Choose two numbers whose sum is -16 and whose product is 48.
These would by -12 and -4.
Then:
