Question

asked Feb 23, 2020 19.3k views

2 Answers

Bschaeffer · Answer 1 · 2020-02-24T11:17:00+0000

set f(x) equal to y

y = 19/ x^3

swap x and y

x = 19/y^3

make y the subject

xy^3 = 19

y^3 = 19/x

$y = \sqrt[3]{ (19)/(x) }$

then just replace y with f^-1(x)

$f(x) = \sqrt[3]{ (19)/(x) }$

hope this helped! have a good day ~ •lipika•

Terence Lewis · Answer 2 · 2020-02-28T17:25:55+0000

Answer:

The inverse of the function F(x) is:

$\sqrt[3]{(19)/(x)}$

We are given a rational function F(x) as:

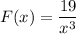
F(x)=(19)/(x^3)

The steps to find the inverse function of a given function f(x) are as follows:

1. Put f(x)=y

2. Interchange the value of x and y

3. Solve for y.

Hence, we find the inverse of F(x) as follows:

F(x)=y

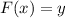
i.e.

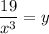
(19)/(x^3)=y

Now we interchange x and y

i.e.

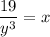
(19)/(y^3)=x

Now we solve for y as follows:

$y^3=(19)/(x)\\\\i.e.\\\\y=\sqrt[3]{(19)/(x)}$

Hence, the inverse function is:

$\sqrt[3]{(19)/(x)}$