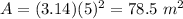PLEASE HELP A plane intersects a cylinder parallel to the cylinder’s bases. What’s the area of the resulting cross section? Use 3.14 for π. Round your answer to the nearest tent…

Question

asked May 13, 2020 192k views

1 Answer

Frankich · Answer 1 · 2020-05-16T13:20:29+0000

Answer:

The area of the resulting cross section is
$78.5\ m^(2)$

Explanation:

we know that

The resulting cross section is a circle congruent with the circle of the base of cylinder

therefore

The area is equal to

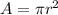
$A=\pi r^(2)$

we have

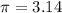
$\pi=3.14$

$r=10/2=5\ m$ -----> the radius is half the diameter

substitute the values

$A=(3.14)(5)^(2)=78.5\ m^(2)$