Question

Question 2: 11 pts

A coin is tossed three times. Find the probability that 2 heads and 1 tail turn up in any order.

Answer 1

3/8 or 0.375 or 37.5%

Explanation:

So since the coin is tossed three times, it's not to hard to write out every scenario since there will only be 2^3 combinations or 8 combinations. But we can also use Binomial Distribution Formula.

Binomial Distribution Formula:

`P(x)=(^n_x)p^xq^(n-x)`

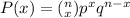
Where p = probability of success and q=probability of failure, x=how many successes, and n=total number of trials

Combination Formula:

`(^n_x) = (n!)/(x!(n-x)!)`

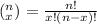
So let's define the variable values, since it's a coin, the probability of heads/tails should be 50/50 so p=0.50 and q=0.50. Since we want 2 heads then x=2, and since the total number of trials is 3, n=3.

So let's plug the values into the equation:

`P(x)=(3!)/(2!)*(0.50)^2*(0.50)^1`

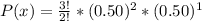
Rewrite 0.50 as a fraction

`P(x)=(3*2*1)/(2*1)*((1)/(2))^2*((1)/(2))^1`

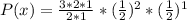
Cancel out values in fraction, and also square the fraction

`P(x)=3*(1)/(4)*(1)/(2)`

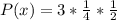
Multiply fractions

`P(x)=3*(1)/(8)`

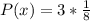
Multiply the two values

`P(x)=(3)/(8)`

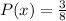
This means the probability is 3/8 or 0.375 or 37.5%

I also provided a diagram on how to just draw out each scenario/combination