Question

HELP!!!!!!! Choose the graph that matches the following system of equations:

4x + 2y = −2 
x − 3y = 24​

Answer 1

The answer in the attached figure

Explanation:

we have

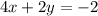`4x + 2y = -2` -----> equation A

`x-3y=24` -----> equation B

Isolate the variable x in the equation B

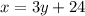`x=3y+24` ----> substitute in the equation A and solve for y

`4(3y+24) + 2y = -2`

`12y+96+ 2y = -2`

`14y = -2-96`

`14y = -98`

`y = -7`

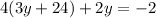
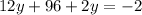
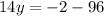
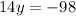
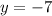
Find the value of x

`x=3(-7)+24=3`

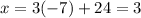
The solution of the system of equations is the point (3,-7)