Question

Find the polar equation of the conic with the focus at the pole, directrix y = -6, and eccentricity 4

Answer 1

B

Explanation:

edge

Answer 2

Choice B is correct

Explanation:

The eccentricity of the conic section is given as 4 and thus the conic section is a hyperbola. Hyperbolas are the only conic sections with an eccentricity greater than 1.

Next, the directrix of this hyperbola is located at y = -6 implying that the hyperbola will be opening upwards. Consequently, the polar equation of this hyperbola will be of the form;

`r=(k)/(1-4sin(theta))`

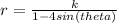
The value of k in the numerator is the product of eccentricity and the absolute value of the directrix;

k= 4*6 = 24

The polar equation is thus given by alternative B