Answer:
The answer is circle; 2(x')² + 2(y')² - 5x' - (5√3)y' - 6 = 0 ⇒ answer (b)
Explanation:
* At first lets talk about the general form of the conic equation
- Ax² + Bxy + Cy² + Dx + Ey + F = 0
∵ B² - 4AC < 0 , if a conic exists, it will be either a circle or an ellipse.
∵ B² - 4AC = 0 , if a conic exists, it will be a parabola.
∵ B² - 4AC > 0 , if a conic exists, it will be a hyperbola.
* Now we will study our equation:
* x² - 5x + y² = 3
∵ A = 1 , B = 0 , C = 1
∴ B² - 4AC = (0) - 4(1)(1) = -4 < 0
∵ B² - 4AC < 0
∴ it will be either a circle or an ellipse
* Lets use this note to chose the correct figure
- If A and C are equal and nonzero and have the same sign,
then the graph is a circle.
- If A and C are nonzero, have the same sign, and are not equal
to each other, then the graph is an ellipse.
∵ A = 1 an d C = 1
∴ The graph is a circle.
* To find its center of the circle lets use
∵ h = -D/2A and k = -E/2A
∵ A = 1 and D = -5 , E = 0
∴ h = -(-5)/2(1) = 2.5 and k = 0
∴ The center of the circle is (2.5 , 0)
* Now lets talk about the equation of the circle and angle Ф
∵ Ф = π/3
- That means the graph of the circle will transformed by angle = π/3
- The point (x , y) will be (x' , y'), where
* x = x'cos(π/3) - y'sin(π/3) , y = x'sin(π/3) + y'cos(π/3)
∵ cos(π/3) = 1/2 and sin(π/3) = √3/2
∴
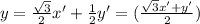
∴
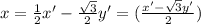
* Lets substitute x and y in the equation x² - 5x + y² = 3
∵
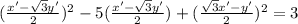
* Lets use the foil method
∴
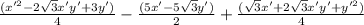 =3
=3
* Make L.C.M
∴
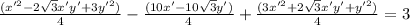
* Open the brackets ∴
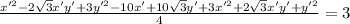
* Collect the like terms
∴

* Multiply both sides by 4
∴ 4(x')² + 4(y')² - 10x' + (10√3)y' = 12
* Divide both sides by 2
∴ 2(x')² + 2(y')² - 5x' + (5√3)y' = 6
∵ h = -D/2A and k = E/2A
∵ A = 2 and D = -5 , E = 5√3
∴ h = -(-5)/2(2) = 5/4 =1.25
∵ k = (5√3)/2(2) = (5√3)/4 = 1.25√3
∴ The center of the circle is (1.25 , 1.25√3)
∵ The center of the first circle is (2.5 , 0)
∵ The center of the second circle is (1.25 , 1.25√3)
∴ The circle translated Left and up
* 2(x')² + 2(y')² - 5x' - (5√3)y' - 6 = 0
∴ The answer is circle; 2(x')² + 2(y')² - 5x' - (5√3)y' - 6 = 0
* Look to the graph
- the purple circle for the equation x² - 5x + y² = 3
- the black circle for the equation (x')² + (y')² - 5x' - 5√3y' - 6 = 0