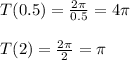Answer:
When b= 0.5, the period of orange graph is _4_ pi
When b= 2, the period of orange graph is _1_pi
Explanation:
The period of the sinusoidal functions can be easily calculated by observing their graphs.
First, look at the orange graph when b = 0.5
Identify a point where the orange chart cuts the x-axis. For example at
 . After completing the rise and fall cycle, the function cuts back to the x axis at
. After completing the rise and fall cycle, the function cuts back to the x axis at
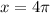 .
.
Then the period
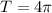 .
.
Second, look at the orange graph when b = 2
Identify a point where the orange chart cuts the x-axis. For example at
 . After completing the rise and fall cycle, the function cuts back to the x-axis at
. After completing the rise and fall cycle, the function cuts back to the x-axis at
 .
.
Then the period
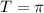 .
.
We also know that the period of a sinusoidal function is defined as
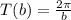
So: