Question

Plz help me

When graphed, which function has a horizontal asymptote at 4?

A.f(x)=2x-4

B.f(x)=2(3^x)+4

C.f(x)=-3x+4

D.f(x)=3(2^x)-4

Answer 1

It is B.

Explanation:

f(x) = 2(3^x) + 4

As x approaches negative infinity 2(3^x) approaches zero and f(x) approaches 4.

Answer 2

B.
`f(x)=2(3^x)+4`

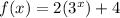
Explanation:

We have to find that which graph has horizontal asymptote at 4

We know that to find the horizontal asymptote , we simply evaluate the limit of the function as it approaches to infinity or it approaches to negative infinity.

A.
`f(x)=2x-4`

`\lim_(x\rightarrow \infty)(2x-4)=\infty`

`\lim_(x\rightarrow -\infty)(2x-4)=-\infty`

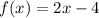
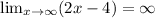
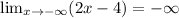
Limit of function does not exits, so function have not horizontal asymptote.

B.
`f(x)=2(3^x)+4`

`\lim_(x\rightarrow \infty)(2(3^x)+4)=\infty`

`3^(\infty)=\infty`

`\lim_(x\rightarrow -\infty)(2(3^x)+4)=4`

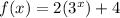
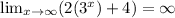
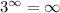
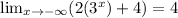
Because
`3^(-\infty)=0`

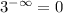
Hence, function have horizontal asymptote at 4.

C.
`f(x)=-3x+4`

`\lim_(x\rightarrow \infty)(-3x+4)=\infty`

`\lim_(x\rightarrow -\infty)(-3x+4)=-\infty`

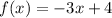
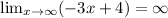
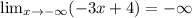
Hence, function have not horizontal asymptote.

D.
`f(x)=3(2^x)-4`

`\lim_(x\rightarrow \infty)(3(2^x)-4)=\infty`

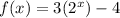
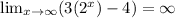
Because
`2^(\infty)=\infty`

`\lim_(x\rightarrow -\infty)(3(2^x)-4)=-4`

`2^(-\infty)=0`

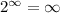
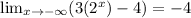
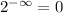
Hence, function have horizontal asymptote at -4.

Therefore, option B is true.