Question

Which of the following is

key property of the quadratic parent function?
A. Its vertex is at the origin.
B. It is not a function.
C. It iS not a parabola.
D It is in quadrants III and IV.

Answer 1

Explanation:

i think it is c

Answer 2

A

Explanation:

So let's look at each and determine whether they're true or not.

A. It's vertex is at the origin:

This is true! The reason for this is because you can express a quadratic in vertex form as such:
`f(x)=a(x-h)+k` where (h, k) is the vertex. If you remember the parent function is simply:
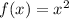`f(x)=x^2` which we can express as:
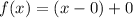`f(x) = (x-0)+0` meaning the vertex is at (0, 0). This also intuitively makes sense, the x^2 will only output positive values for real numbers, so when x<0, f(x) is still going to be positive because it's squaring the negative, so that means when you go from -5 to -4, even though you increased x by 1, the f(x) decreases by 1, since it's squaring the value to get a positive value. The lowest value this can output is 0 because 0^2 = 0. This means you vertex is at the origin.

B. It is not a function:

So the quadratic parent function only outputs 1 value for each input, although it isn't a one-to-one function, meaning that each output isn't unique, but each input still only outputs 1 output, which makes this a function

C. It is not a parabola:

parabolas are expressed as quadratic equations, so this is false.

D. It is in quadrants ||| and IV:

This is not true since the parent function opens upwards and has a vertex at (0, 0) so it will only be in quadrant I and II. I'll provide a diagram showing this.