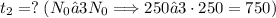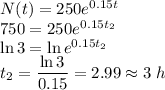Answer:
a)
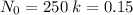
b) 334,858 bacteria
c) 4.67 hours
d) 2 hours
Step-by-step explanation:
a) Initial number of bacteria is the coefficient, that is, 250. And the growth rate is the coefficient besides “t”: 0.15. It’s rate of growth because of its positive sign; when it’s negative, it’s taken as rate of decay.
Another way to see that is the following:
Initial number of bacteria is N(0), which implies
 . And
. And
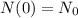 . The process is:
. The process is:
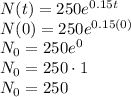
b) After 2 days means
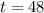 . So, we just replace and operate:
. So, we just replace and operate:
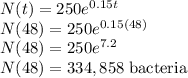
c)
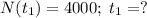
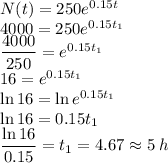
d)