Question

A right triangle has legs measuring 4.5 meters and 1.5 meters. The length of a second triangle are proportional to the lengths of the legs of the first triangle. Which could be the length of the legs of the second triangle? A) 6m and 2m B) 8m and 5m C) 7m and 3.5m D) 10m and 2.5m E) 11.25 and 3.75m

Answer 1

A. 6m and 2m

E. 11.25m and 3.75m

Explanation:

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional

so

Verify each case

case A) 6m and 2m

`(6)/(4.5)=(2)/(1.5) \\ \\6(1.5)=2(4.5)\\ \\9=9`

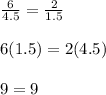
therefore

The legs are proportional

case B) 8m and 5m

`(8)/(4.5)=(5)/(1.5) \\ \\8(1.5)=5(4.5)\\ \\12\\eq22.5`

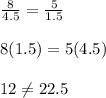
therefore

The legs are not proportional

case C) 7m and 3.5m

`(7)/(4.5)=(3.5)/(1.5) \\ \\7(1.5)=3.5(4.5)\\ \\10.5\\eq15.75`

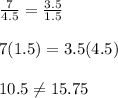
therefore

The legs are not proportional

case D) 10m and 2.5m

`(10)/(4.5)=(2.5)/(1.5) \\ \\10(1.5)=2.5(4.5)\\ \\15\\eq11.25`

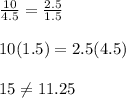
therefore

The legs are not proportional

case E) 11.25m and 3.75m

`(11.25)/(4.5)=(3.75)/(1.5) \\ \\11.25(1.5)=3.75(4.5)\\ \\16.875=16.875`

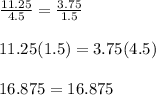
therefore

The legs are proportional