Well we can't do all of those for you, how about a sampling.
In 14 and 15 we'll have a tangent whenever the radius and the associated purported tangent meet at a right angle. We have the right angle sign on 14 and not 15, so the answer is probably 14. YES, 15. NO. We can check with the Pythagorean Theorem:
14.
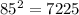
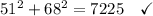
Those match, so we have a right angle B, so answer is YES
15.
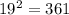
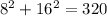
Those are different, B is not a right angle, so answer NO
16.
It would be helpful if they labeled some points. Let's call the tangent point T, the other end of the chord U and the center C.
If we draw triangle TCU, the central angle TCU=128 degrees, because that's what the measure of the arc means.
Our triangle is isosceles because CT and CU are both radii. So the angles CTU and CUT are congruent, so both must be
CTU = CUT = (180 - 128)/2 = 26 degrees
Angle 1 is angle CTU + 90 degrees, because the tangent always makes a 90 degree angle with the radius. Angle 2 is the supplement of angle 1.
Answer: Angle 1 = 90+26 = 116 degrees. Angle 2 = 180-116 = 64 degrees
Three's the limit around here so I'll leave the rest to you.