Answer:
The equation is that of ellipse withe angle of rotation 30° ⇒ answer (d)
Explanation:
* Lets talk about the general form of the conic equations
- Ax² + Bxy + Cy² +D = 0 (center is the origin)
- A is the coefficient of x² , B is the coefficient of xy
C is the coefficient of y² , D is the numerical term
* Now we will study how to know the type of the graph of this equation
- If A and C have different signs (different values)
∴ The equation is that of an ellipse
- If A and C have different signs (different values)
∴ The equation is on a hyperbola
* Now look at the equation:
13x² + 6√3 xy + 7y² - 16 = 0
∵ A = 13 , B = 6√3 , C = 7 , D = -16
∵ A and C have same sign
∴ The equation is that of an ellipse
* Now lets find the angle of rotation by using the Rule:
- tan(2Ф) = B/(A - C) ⇒ Ф is the angle of rotation
- By using the value of A , B and C
∴ tan(2Ф) = 6√3/(13 - 7) = 6√3/6 = √3
∴ 2Ф =
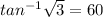
∴ 2Ф = 60° ⇒ divide both sides by 2
∴ Ф = 30°
∴ The angle of rotation is 30°
∴ The equation is that of ellipse withe angle of rotation 30°
* The graph represent the ellipse
- The purple line represents the angle of rotation