Answer:
The answer is hyperbola; (x')² - (y')² - 16 = 0 ⇒ answer (a)
Explanation:
* At first lets talk about the general form of the conic equation
- Ax² + Bxy + Cy² + Dx + Ey + F = 0
∵ B² - 4AC < 0 , if a conic exists, it will be either a circle or an ellipse.
∵ B² - 4AC = 0 , if a conic exists, it will be a parabola.
∵ B² - 4AC > 0 , if a conic exists, it will be a hyperbola.
* Now we will study our equation:
xy = -8
∵ A = 0 , B = 1 , C = 0
∴ B² - 4 AC = (1)² - 4(0)(0) = 1 > 0
∴ B² - 4AC > 0
∴ The graph is hyperbola
* The equation xy = -8
∵ We have term xy that means we rotated the graph about
the origin by angle Ф
∵ Ф = π/4
∴ We rotated the x-axis and the y-axis by angle π/4
* That means the point (x' , y') it was point (x , y)
- Where x' = xcosФ - ysinФ and y' = xsinФ + ycosФ
∴ x' = xcos(π/4) - ysin(π/4) , y' = xsin(π/4) + ycos(π/4)
∴ x' = x/√2 - y/√2 = (x - y)/√2
∴ y' = x/√2 + y/√2 = (x + y)/√2
* Lets substitute x' and y' in the 1st answer
∵ (x')² - (y')² - 16 = 0
∴
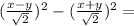
(

* Lets open the bracket
∴
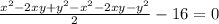
* Lets add the like terms
∴
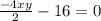
* Simplify the fraction
∴ -2xy - 16 = 0
* Divide the equation by -2
∴ xy + 8 = 0
∴ xy = -8 ⇒ our equation
∴ Answer (a) is our answer
∴ The answer is hyperbola; (x')² - (y')² - 16 = 0
* Look at the graph:
- The black is the equation (x')² - (y')² - 16 = 0
- The purple is the equation xy = -8
- The red line is x'
- The blue line is y'