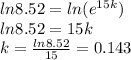Answer:
Choice A
Explanation:
The scenario presented relates to exponential growth models; the population of bacteria is growing at an exponential rate given by the equation;
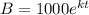
In this case B represents the population of the bacteria, t the time in minutes, k the growth constant and 1000 represents the initial population at time 0.
After 15 minutes, the population of bacteria grows to 8520. This implies that B is 8520 while t is 15. We substitute this values into the given equation and solve for k, the growth constant;
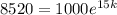
Divide both sides by 1000;
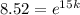
The next step is to introduce natural logs on both sides of the equation;