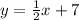Question

Which is the equation in the slope-intercept form for the line that passed through (2, 8) And it is perpendicular to 4x + 2y= 6?

Answer 1

Answer:
`y=(1)/(2)x+7`

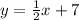
Explanation:

The slope-intercept form of the equation of the line is the following:

`y=mx+b`

Where m is the slope and b the y-intercept.

By definition, when two lines are perpendicular, their slopes are opposite reciprocals.

Then, to find the slope of the equation of the line given, you can solve for y:

`4x+2y=6\\2y=-4x+6\\\\y=-2x+3`

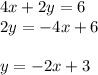
As you can see, the slope of this line is -2.Then, the slope of the line that is perpendicular to it, must be:

`m=(1)/(2)`

Substitute the slope and the point given, into the equation and solve for b:

`8=(1)/(2)(2)+b\\8=1+b\\b=7`

Therefore, the equation of this line is:

`y=(1)/(2)x+7`