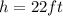Question

HELP PLEASE!! As John walks 16 ft towards a chimney, the angle of elevation from his eye to the top of the chimney changes from 30° to 45°. Identify the height of the chimney from John's eye level to the top of the chimney rounded to the nearest foot.

Answer 1

Answer: 22 feet.

Explanation:

Note that there are two right triangles in the figure attached: ACD and BCD. Where "h" is the height of the chimeney from John's eye level to the top of the chimney.

You need to use the trigonometric identity
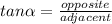`tan\alpha=(opposite)/(adjacent)` for this exercise.

• For the triangle BCD:

`tan(45\°)=(h)/(x)`

Solve for h:

`h=xtan(45\°)\\h=x`

• For the triangle ACD:

`tan(30\°)=(h)/(x+16)`

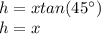
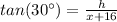
Substitute
`h=x` and solve for h:

`tan(30\°)=(h)/(h+16)\\\\(h+16)(tan(30\°))=h\\\\0.577h+9.237=h\\\\9.237=h-0.577h\\\\9.237=0.423h\\\\h=(9.237)/(0.423)\\\\h=21.836ft`

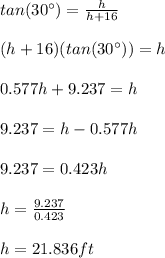
Rounded to the nearest foot:

`h=22ft`