Answer:
The ratio of the amount of the 30% solution to the amount of 5% solution will be 1 : 4.
Explanation:
Suppose, the amount of 30% acid solution is
 and the amount of 5% acid solution is
and the amount of 5% acid solution is
 .
.
So, the total amount of the mixture
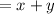 , which is 10% acid solution.
, which is 10% acid solution.
Amount of acid in 30% solution

Amount of acid in 5% solution
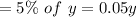
Amount of acid in the mixture
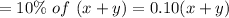
Now, the equation will be......
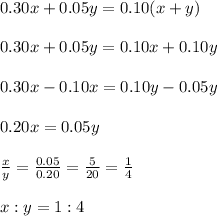
So, the ratio of the amount of the 30% solution to the amount of 5% solution will be 1 : 4.