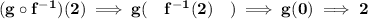Question

I need help with question 9

Answer 1

let's not forget that a function and its inverse have a domain <-> range relationship, namely, if the original function has a point of say (3 , 7 ), then its inverse function will have a point of (7 , 3 ), the same pair just flipped sideways.

`\bf (g\circ f^(-1))(x)\implies g(~~~f^(-1)(x)~~~) \\\\\\ (g\circ f^(-1))(2)\implies g(~~~f^(-1)(2)~~~) \\\\[-0.35em] ~\dotfill\\\\ \textit{so let's firstly find out what is }f^(-1)(2)`

we don't have an f⁻¹(x), darn!! but but but, we do have an f(x) on the left-hand-side graph, and it has a pair where y = 2, namely ([ ] , 2), so then, f⁻¹(x) will have the same pair but sideways, let's inspect f(x).

hmmmmmm when y = 2, x = 0, notice the y-intercept on the graph, ( 0, 2 ).

so then, that means that f⁻¹(x) has a pair sideways of that, namely ( 2, 0), or f⁻¹(2) = 0.

so then, g( f⁻¹(2) ), is really the same as looking for g( 0 ), well then, what is "y" when x = 0 on g(x)? let's inspect the right-hand-side graph.

hmmmmmmmmmmm notice, the point is at ( 0 , 2 ), namely when x = 0, y = 2.

`\bf (g\circ f^(-1))(2)\implies g(~~~f^(-1)(2)~~~)\implies g(0)\implies 2`