Hello!
The graph is attached.
To graph a parabola we need to know the following:
- If the parabola is open upwards or downwards
- They axis intercepts (if they exist)
- The vertex position (point)
We are given the function:

Where,
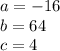
For this case, the coefficient of the quadratic term (a) is negative, it means that the parabola opens downwards.
Finding the axis interception points:
Making the function equal to 0, we can find the x-axis (t) intercepts, but since the equation is a function of the time, we will only consider the positive values, so:
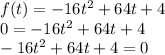
Using the quadratic equation:

So, at t=4.0615 the height of the softball will be 0.
Since we will work only with positive values of "x", since we are working with a function of time:
Let's start from "t" equals to 0 to "t" equals to 4.0615.
So, evaluating we have:
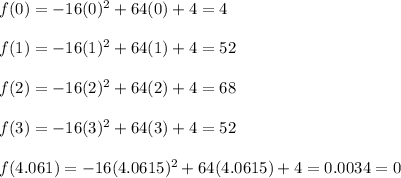
Finally, we can conclude that:
- The softball reach its maximum height at t equals to 2. (68 feet)
- The softball hits the ground at t equals to 4.0615 (0 feet)
- At t equals to 0, the height of the softball is equal to 4 feet.
See the attached image for the graphic.
Have a nice day!