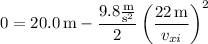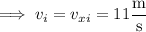The ball's horizontal and vertical velocities at time
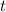 are
are
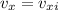
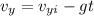
but the ball is thrown horizontally, so
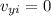 . Its horizontal and vertical positions at time
. Its horizontal and vertical positions at time
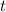 are
are
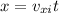
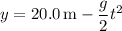
The ball travels 22 m horizontally from where it was thrown, so
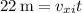
from which we find the time it takes for the ball to land on the ground is
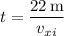
When it lands,
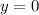 and
and