Question

Consider the population of all 1-gal cans of dusty rose paint manufactured by a particular paint company. Suppose that a normal distribution with mean μ = 5 ml and standard deviation σ = 0.2 ml is a reasonable model for the distribution of the variable x = amount of red dye in the paint mixture. Use the normal distribution model to calculate the probabilities below. (Round all answers to four decimal places.)

(a) P(x > 5) =
(b) P(x < 5.4)=

(c) P(x lteq.gif 5.4) =

(d) P(4.6 < x < 5.2) =

(e) P(x > 4.5) =

(f) P(x > 4) =

Answer 1

A) 0.5000; B) 0.9772; C) 0.9772; D) 0.8185; E) 0.9932; F) 1.0000

Explanation:

For each of these, we will use a z score. The formula for a z score is:

`x=(X-\mu)/(\sigma)`

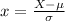
A) Our X is 5, our mean is 5 and our standard deviation is 0.2:

z = (5-5)/(0.2) = 0/0.2 = 0

Using a z table, the value to the left of this, less than, is 0.5000; this means the area to the right of this, greater than, is 1-0.5000 = 0.5000.

B) Our X is 5.4, the mean is 5 and the standard deviation is 0.2:

z = (5.4-5)/0.2 = 0.4/0.2 = 2

Using a z table, the value to the left of this, less than, is 0.9772.

C) The probability for this will be the same as for B; there is no distinction between "less than" and "less than or equal to" in z tables.

D) We find the z score for each of the endpoints of this interval, find the probabilities and subtract them:

z = (4.6-5)/0.2 = -0.4/0.2 = -2; the probability is 0.0228.

z = (5.2-5)/0.2 = 0.2/0.2 = 1; the probability is 0.8413.

The area between them is 0.8413-0.0228 = 0.8185.

E) X is 4.5, the mean is 5 and the standard deviation is 0.2:

z = (4.5-5)/0.2 = -0.5/0.2 = -2.5; the probability less than this is 0.0062. This means the probability greater than this is 1-0.0062 = 0.9938.

F) X is 4, the mean is 5 and the standard deviation is 0.2:

z = (4-5)/0.2 = -1/0.2 = -5. Everything in the z table is larger than this, so the probability is 1.000.