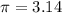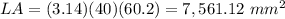Question

In a chemistry lab experiment, you use the conical filter funnel shown at the right. How much filter paper do you need to line the funnel?

Answer 1

`7,561.12\ mm^(2)`

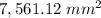
Explanation:

we know that

The lateral area of a cone is equal to

`LA=\pi rl`

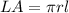
where

r is the radius of the base

l is the slant height

we have

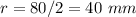`r=80/2=40\ mm` ----> the radius is half the diameter

`h=45\ mm`

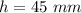
To find the slant height apply the Pythagoras theorem

`l^(2)=r^(2)+h^(2)`

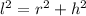
substitute the values

`l^(2)=40^(2)+45^(2)`

`l^(2)=3,625`

`l=60.2\ mm`

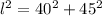
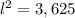
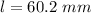
Find the lateral area

assume
`\pi=3.14`

`LA=(3.14)(40)(60.2)=7,561.12\ mm^(2)`