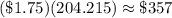1 Answer

Sam Arul Raj T · Answer 1 · 2020-01-07T20:53:49+0000

Answer:

$357

Explanation:

We have a rectangle measuring 25 feet × 9 feet. Remove from the rectangle two regular hexagons with a side length equal to 2 feet.

The formula of an area of a rectangle:

A_r=lw

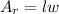
l - length, w - width.

Substitute l = 25 ft and w = 9 ft:

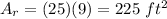
$A_r=(25)(9)=225\ ft^2$

The formula of an area of a regular hexagon:

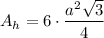
$A_h=6\cdot(a^2\sqrt3)/(4)$

a - side

Substitute a = 2 ft:

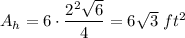
$A_h=6\cdot(2^2\sqrt6)/(4)=6\sqrt3\ ft^2$

The area of the wall:

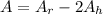
A=A_r-2A_h

Substitute:

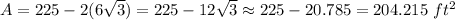
$A=225-2(6\sqrt3)=225-12\sqrt3\approx225-20.785=204.215\ ft^2$

Paiting the wall costs $1.75 per ft². Calculate:

$(\$1.75)(204.215)\approx\$357$