Question

Amy scores an 82% on her math test with Ms. Smith. The average score for her class is a 75% with a standard deviation of 2%. Amy’s friend Karina is taking the same test with Mr. Adams. His class average is a 73% and a standard deviation of 3%. What is the lowest score Karina needs to score higher than Amy relative to the class distributions?

Answer 1

Assuming scores are normally distributed, a score of 82% on Ms. Smith's test corresponds to the
`p`-th percentile, i.e.

`P(X_S\le82)=p`

where
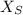`X_S` is a random variable denoting scores on Ms. Smith's test.

Transform
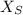`X_S` to
`Z`, which follows the standard normal distribution:

`P(X_S\le82)=P\left(\frac{X_S-75}2\le\frac{82-75}2\right)=P(Z\le3.5)\approx0.9998`

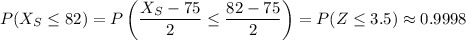
which means Amy scored at the 99.98th percentile.

This makes it so that Karina needs to score
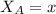`X_A=x` on Mr. Adams' test so that

`P(X_A\le x)=0.9998`

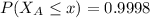
Their test scores have the same
`z` score computed above, so

`\frac{x-73}3=3.5\implies x=83.5`

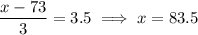
so Karina needs to get a test score of at least 83.5%.

Answer 2

the answer is 84%

Explanation: