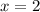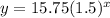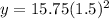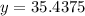Answer:
x y
-2 7
-1 10.5
0 15.75
1 23.625
2 35.4375
Explanation:
The general equation of the exponential function is
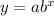 .
.
We know from our table that when
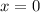 ,
,
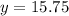 . Let's replace those values in our equation:
. Let's replace those values in our equation:
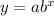
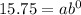
Remember that
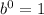 , so:
, so:
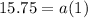
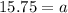
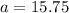
We also know from our table that when
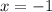 ,
,
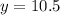 . Let's replace the values again:
. Let's replace the values again:
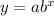
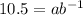
But we now know that
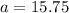 , so let's replace that value as well:
, so let's replace that value as well:
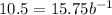
Remember that
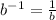 , so:
, so:
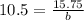
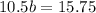
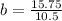
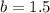
Now, we can put it all together to complete our exponential function:
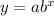
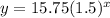
To find the missing values, we just need to evaluate our function at
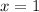 and
and
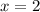 :
:
- For
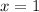
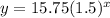
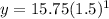
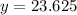
- For