Question

A survey was done of 902 students. The mean of their results was 26 and the standard deviation was 4. How many students responded above 35?

Answer 1

the answer is 11

Explanation:

Answer 2

11 students out of 902 responded above 35

Explanation:

Using z-score we can find what percentage of student will be above 35. Using this percentage we can calculate how many students out of 902 scored above 35.

Mean = u = 26

Standard deviation = s = 4

Target Value = x = 35

Formula for the z score is:

`(x-u)/(s)`

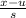
Using the values in this formula, we get:

`(35-26)/(4) =2.25`

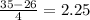
Using the z table we can find the percentage of values that would be 2.25 standard deviations above the mean in a normal distribution. Using the z-table we get this value to be 0.0122 or 1.22%

Thus 1.22% of the values will be above 35.

1.22% of 902 is 11 (rounded to nearest whole number)

Thus 11 students out of 902 responded above 35