Question

∑

∞
n
=
1
−
4
(
1
3
)
n
−
1

Answer 1

6

Explanation:

The correct notation is: Summation from n = 1 to infinity of the expression:

`4((1)/(3) )^(n-1)`

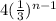
If we expand this notation, we will find that the given summation represent the terms of a G.P and we have to find the sum of infinite terms of a G.P. By placing n=1,2,3,4,... we can find the first few terms as shown below:

`4((1)/(3) )^(1-1)=4\\\\ 4((1)/(3) )^(2-1)=4((1)/(3) ) \\\\ 4((1)/(3) )^(3-1) =4((1)/(3) )^(2)`

Its obvious from the above result, that the given summation represent a G.P with first term equal to 4 and common ratio of 1/3. The formula of infinite G.P is:

`S=(a_(1) )/(1-r)`

Using the value of a1 = 4 and r = 1/3 we can calculate the given summation

`S=(4)/(1-(1)/(3) )=6`

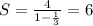
Therefore, the given summation is equal to 6.