Question

Select the correct slope calculation for the line that contains the points in the table.

Answer 1

Answer: Your correct answer should be C,
`((9 - (-3)))/((1 - (-2)))`

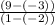
Explanation:

Recall the slope equation is: (y2 - y1)/(x2 - x1) or
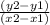`((y2 - y1))/((x2 - x1))`. You need two points: point one (x1, y1) and point two (x2, y2).

* The first answer choice is flawed because not only is it in a different formula (xs are in the numerator instead of the denominator area), but it says 1 - 2 when it should be 1 - (-2) or 1 + 2.

* The second answer choice is flawed because it is in a different formula (this time, x1 - x2/y3 - y2) and 2 - 1 is suppose to be -2 - 1.

* The last answer is flawed because it should be -3 - (-) 11 and -2 - (-)4, or -3 + 11 and -2 + 4.

Note: If you had a negative operation and a negative number behind it, you can either formulate the equation like x - (-) y or drop the negative sign from said number and change the minus operation sign to the plus one (x + y).

The only answer choice that checks out and is not flawed is C.

Answer 2

Answer: option c

Explanation:

By definition, you can calculate the slope of line by applying the formula shown below:

`m=(y_2-y_1)/(x_2-x_1)`

Then:

You can see that in the option C the equation of the slope is applied correctly:

`(9-(-3))/(1-(-2))`

Where:

`y_2=9\\y_1=-3\\\\x_2=1\\x_1=-2`

Then, you obtain the following value of the slope of the line:

`m=(9-(-3))/(1-(-2))=4`