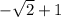Question

Find the exact value by using a half-angle identity.

tangent of seven pi divided by eight

tan (7pi/8)

please show step by step

Answer 1

The exact form of
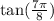`\tan((7\pi)/(8))` is
`-√(2)+1`

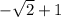
Explanation:

We need to find the exact value of
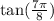`\tan((7\pi)/(8))` using half angle identity.

Since,
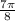`(7\pi)/(8)` is not an angle where the values of the six trigonometric functions are known, try using half-angle identities.

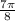`(7\pi)/(8)` is not an exact angle.

First, rewrite the angle as the product of
`(1)/(2)` and an angle where the values of the six trigonometric functions are known. In this case,

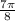`(7\pi)/(8)` can be written as ;

`((1)/(2))(7\pi)/(4)`

Use the half-angle identity for tangent to simplify the expression. The formula states that
`\tan (\theta)/(2)=(\sin \theta)/(1+ \cos \theta)`

`=(\sin((7\pi)/(4)))/(1+ \cos ((7\pi)/(4)))`

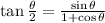
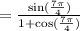
Simplify the numerator.

`=((-√(2))/(2))/(1+ \cos ((7\pi)/(4)))`

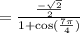
Simplify the denominator.

`=((-√(2))/(2))/((2+√(2))/(2))`

Multiply the numerator by the reciprocal of the denominator.

`(-√(2))/(2)* (2)/(2+√(2))`

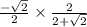
cancel the common factor of 2.

`(-√(2))/(1)* (1)/(2+√(2))`

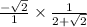
Simplify,

`(-√(2)(2-√(2)))/(2)`

`(-(2√(2)-√(2)√(2)))/(2)`

`(-(2√(2)-2))/(2)`

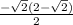
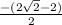
simplify terms,

`-√(2)+1`

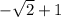
Therefore, the exact form of
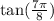`\tan((7\pi)/(8))` is
`-√(2)+1`