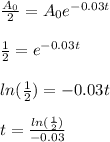Question

a certain isotope decays so that the amount A remaining after t years is given by: A=A0 x e^-0.03t, where A0 is the original amount of the isotope. to the nearest year, the half-life of the isotope (the amount of the time it takes to decay to half the original amount) is ____ years

Answer 1

`t = 23.10\ years`

Explanation:

We have an exponential decay function:

`A = A_0e ^(-0.03t)`

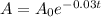
This function decreases as the years pass. That is, if A is the quantity for a time t and
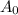`A_0` is the original quantity at time t = 0 then:

`A <A_0`

We want to know for what value of t the value of A decreases by half of
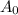`A_0`. That is, we want to know when
`A = (A_0)/(2)`

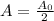
Then we do:

`(A_0)/(2) = A_0e ^(-0.03t)\\\\(1)/(2) =e ^(-0.03t)\\\\ln((1)/(2)) = -0.03t\\\\t = (ln((1)/(2)))/(-0.03)`

`t = 23.10\ years`