Question

Use the laws of logarithms and the values given below to evaluate the logarithmic expression (picture provided)

Answer 1

Factor out 8 using 2.

log(8) = log(2^3)

Use the product rule [ log(xy) = log(x) + log(y) ] to simplify.

log(2^3) = 3 log(2)

Simplify using the given value for 2.

3(0.3010)

0.9030

Therefore, log(8) ≈ 0.9030 (Option B)

Best of Luck!

Answer 2

Answer: option b.

Explanation:

To solve the given exercise, you must keep on mind the following law of logaritms:

`m*log(a)=log(a)^m`

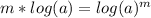
Descompose 8 into its prime factors:

`8=2*2*2=2^3`

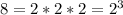
Therefore, you can rewrite the expression given, as following:

`log8=log2^3=3log2`

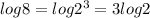
You know that
`log2=0.3010`

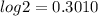
Then, when you substitute, you obtain:

`3*0.3010`≈0.9030