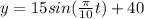Question

The blades of a windmill turn on an axis that is 40 feet from the ground. The blades are 15 feet long and complete 3 rotations every minute. Write a sine model, y = asin(bt) + k, for the height (in feet) of the end of one blade as a function of time t (in seconds). Assume the blade is pointing to the right when t = 0 and that the windmill turns counterclockwise at a constant rate.

a is the ___
The vertical shift, k, is the _____________
a =
k =

Answer 1

a is the length of the blade

the vertical shift , k, is the height of the windmill

a= 15 k= 40

the period is 20 seconds

b = pi/10

y=15sin(π/10t)+40

Explanation:

Answer 2

a is the _amplitude_(Length of the blades)_

The vertical shift, k, is the _Mill shaft height_

`a = 15\ ft\\\\k = 40\ ft`

`y = 15sin((\pi)/(10)t) + 40`

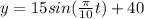
Explanation:

In this problem the amplitude of the sinusoidal function is given by the length of the blades.

`a = 15\ ft`

The mill is 40 feet above the ground, therefore the function must be displaced 40 units up on the y axis. So:

`k = 40\ ft`

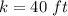
We know that the blades have an angular velocity w = 3 rotations per minute.

One rotation =
`2\pi`

1 minute = 60 sec.

So:

`w = (3(2\pi))/(60)\ rad/s`

`w = (\pi)/(10)\ rad/s`

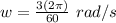
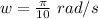
Finally:

a is the _amplitude_(Length of the blades)_

The vertical shift, k, is the _Mill shaft height_

`a = 15\ ft\\\\k = 40\ ft`

`y = 15sin((\pi)/(10)t) + 40`