Question

in a right circular cylinder of height 2 meters, if the volume is increasing at 10 m^3/min how fast is the radius of the cylinder increasing when the radius is 4in?

Answer 1

Given dimensions:

Height of the cylinder = 2 m

Volume is increasing at a rate of = 10 m³/min

Radius = 4 inches

Converting radius in meters.

1 inch = 0.0254 meters

4 inches =
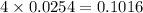`4*0.0254=0.1016` meters

`(dv)/(dt)=10`

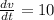
we have to find,
`(dr)/(dt)=?`

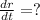
Volume of the cylinder is given by
`\pi r^(2) h`

=
`\pi r^(2) *2 = 2\pi r^(2)`

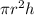
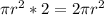
Now differentiating with respect to 't'

`(dv)/(dt) = (d)/(dt) (2\pi r^(2))`

`(dv)/(dt) = 2\pi (2r)((dr)/(dt))`

`10=2\pi (2*0.1016)(dr)/(dt)`

`10=2*3.14(0.2032)(dr)/(dt)`

`(dr)/(dt)=(10)/(1.276)`

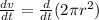
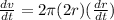
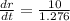
= 7.83 meter per minute.