Answer:
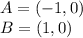
Explanation:
The transformation of the segment AB is:
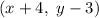
Given the points of the line segment A'B':
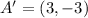 and
and
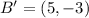
The coordinates of the points A and B in the line segment AB,can be calculated through this procedure:
For A:
x-coordinate:
Substitute the x-coordinate of A' (we can represent it with
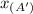 ) into
) into
 and solve for
and solve for
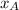 , which is the x-coordinate of A:
, which is the x-coordinate of A:
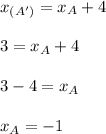
y-coordinate:
Substitute the y-coordinate of A' (we can represent it with
 ) into
) into
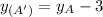 and solve for
and solve for
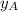 , which is the y-coordinate of A:
, which is the y-coordinate of A:
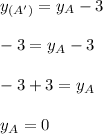
The point of A is: (-1,0)
For B:
x-coordinate:
Substitute the x-coordinate of B' (we can represent it with
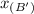 ) into
) into
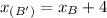 and solve for
and solve for
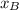 , which is the x-coordinate of B:
, which is the x-coordinate of B:
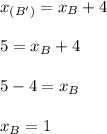
y-coordinate:
Substitute the y-coordinate of B' (we can represent it with
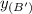 ) into
) into
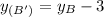 and solve for
and solve for
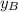 , which is the y-coordinate of B:
, which is the y-coordinate of B:
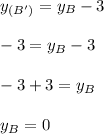
The point of B is: (1,0)