Answer:

Explanation:
Givens:
- Phillip needs at least 200 roses.
- There will be 24 roses per centerpiece.
- There will be 10 roses per bouquet.
 represent the number centerpieces, and
represent the number centerpieces, and
 represents the number of bouquets.
represents the number of bouquets.
According to the problem, we can define the number of roses per a centerpiece:
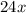
The number of roses per bouquet:
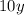
So, the problem restricts the amount of roses, at least 200, that means, 200 or more than 200 roses. Therefore the expression that represent the amount of roses would be:

As you can observe, the inequality includes the 200 roses restriction, and the amount of roses per centerpieces and per bouquet.