Answer: The maximum height of the ball is 0.87 m
Step-by-step explanation:
To calculate the height of the ball, we use third equation of motion:
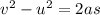
where,
s = distance traveled / height of the ball = ?
u = initial velocity of the ball = 8.30 m/s
v = final velocity of the ball = 7.20 m/s
a = acceleration due to gravity =
 (negative sign represents the ball is going upwards that is against gravity)
(negative sign represents the ball is going upwards that is against gravity)
Putting values in above equation, we get:
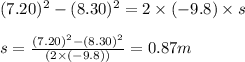
Hence, the maximum height of the ball is 0.87 m