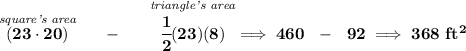Question

Find the area of the irregular figure. I've been stuck on this for awhile. Please help and explain how you did it.

​

Answer 1

to the risk of sounding redundant, as the previous posting is absolutely correct.

Check the picture below.

we know the circum-inscribing figure is a square, namely a 23x20, so it has an area of 23*20 = 460 ft².

the distance from the bottom up, is 20, however to the tip of the triangle is 12, so the diffference is 20 - 12 = 8, meaning the triangle, in yellow, has a height/altitude of 8 ft, and we know its base is 23 ft.

so if we simply take the whole area of the square, and then subtract the area of the triangle, we're in effect making a whole in the squarish area, and what's leftover is the shaded area.

`\bf \stackrel{\textit{square's area}}{(23\cdot 20)}~~~~-~~~~\stackrel{\textit{triangle's area}}{\cfrac{1}{2}(23)(8)}\implies 460~~-~~92\implies 368~ft^2`

Answer 2

Answer: 368 ft^2

Step-by-step explanation:

Pretend it is a square and multiply both sides (23*20=460). The triangle that is cut out has an area of 92 (23*8/2). We know the height of the triangle is 8 because 20-12. We subtract 460-92 and get our answer. :)