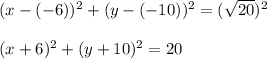Answer:
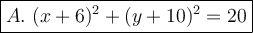
Explanation:
The standard form of an equation of a circle:
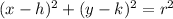
(h, k) - center
r - radius
We have the endpoints of the diameter of a circle (-8, -6) and (-4, -14).
The midpoint of a diameter is a center of a circle.
The formula of a midpoint:
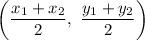
Substitute:
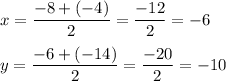
We have h = -6 and k = -10.
The radius is the distance between a center and the point on a circumference of a circle.
The formula of a distance between two points:
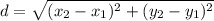
Substitute (-6, -10) and (-8, -6):
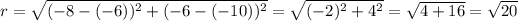
Finally we have