Answer: OPTION C
Explanation:
To solve this problem you must apply the proccedure shown below:
- Use the following formula for calculate the measure fo the central angle:
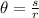
Where s is the arc length and r is the radius.
- Know the lenght of the arc and the radius, you can substitute values.
Therefore, you obtain;
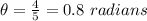
Convert to degrees:
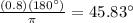 ≈46°
≈46°