Question

If aₙ = 3(3)ⁿ⁻¹ , what is S₃?

12

27

9

39

Answer 1

The correct answer is last option 39

Explanation:

It is given that,

aₙ = 3(3)ⁿ⁻¹

To find a₁

a₁ = 3(3)¹⁻¹ = 3(3)°

= 3 * 1 = 3

To find a₂

a₂ = 3(3)²⁻¹ = 3(3)¹

= 3 * 3 = 9

To find a₃

a₃ = 3(3)³⁻¹ = 3(3)²

= 3 * 9 = 27

To find the value of S₃

S₃ = a₁ + a₂ + a₃

= 3 + 9 + 27 = 39

Therefore the correct answer is last option 39

Answer 2

`S_3=39`

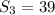
Explanation:

The nth term of the sequence is

`a_n=3(3)^(n-1)`

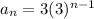
To get the first term, substitute n=1,

`a_1=3(3)^(1-1)=3`

To get the second term, substitute n=2,

`a_2=3(3)^(2-1)=9`

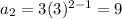
To get the third term, substitute n=3,

`a_3=3(3)^(3-1)=27`

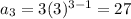
The sum of the first three terms is

`S_3=3+9+27=39`

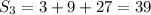
We could also use the formula

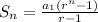`S_n=(a_1(r^n-1))/(r-1)` to get the same result.