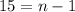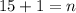Question

How many terms are in the following sequence?

14348907, ..., 9, 3, 1

17

15

16

18

Answer 1

There are 16 terms in the sequence.

Explanation:

The given sequence is

14348907, ..., 9, 3, 1

The first term of the sequence is

`a_1=14348907`

The last term of the sequence is
`l=1`

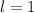
The common ratio is
`r=(1)/(3)`

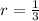
The nth term of this sequence is;

`a_n=a_1(r)^(n-1)`

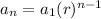
We plug in the common ratio and the first term to get;

`a_n=14348907((1)/(3))^(n-1)`

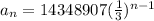
The find the number of terms in the sequence , we plug in the last term of the sequence.

This implies that;

`1=14348907((1)/(3))^(n-1)`

`(1)/(14348907)=((1)/(3))^(n-1)`

`\Rightarrow 3^(-15)=3^(-(n-1))`

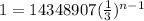
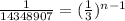
Since the bases are the same, we equate the exponents;

`-15=-(n-1)`

`15=n-1`

`15+1=n`

`n=16`