For this case we must simplify the following expression:
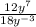
We have that by definition of properties of powers, it is fulfilled that:
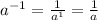
Then, we can rewrite the expression:

By definition of multiplication properties of powers of the same base we have:
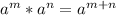
So:
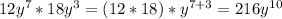
Answer:
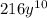
When y = 0 the expression is 0